Collimator vs JModelica

Struggling to choose between Collimator and JModelica? Both products offer unique advantages, making it a tough decision.

Collimator is a Science & Engineering solution with tags like optics, physics, alignment, filtering.

It boasts features such as Aligns radiation beams to shape the beam as needed for different applications, Filters out radiation particles outside of the desired beam shape, Adjustable collimator leaves to customize beam shape, Light field projection to visualize beam shape on patient, Auto-positioning of leaves based on treatment plan and pros including Precisely shapes radiation dose to target tumor while avoiding healthy tissue, Reduces radiation exposure and side effects, Improves treatment accuracy and efficacy, Easy to use and adjust beam shaping leaves, Automated leaf positioning saves time.

On the other hand, JModelica is a Development product tagged with modelica, modeling, simulation, dynamic-systems, differential-equations, algebraic-equations, discrete-equations, open-source.

Its standout features include Modeling and simulation of dynamic systems, Support for Modelica modeling language, Optimization and symbolic algorithms, Model export to FMI and Modelica, Integration with Python and Jupyter notebooks, Open source and cross-platform, and it shines with pros like Free and open source, Support for large and complex models, Fast simulation of hybrid systems, Seamless Python integration, Active development community.

Feature	Collimator	JModelica
Overall Score	N/A	N/A
Primary Category	Science & Engineering	Development

Product Overview

Collimator

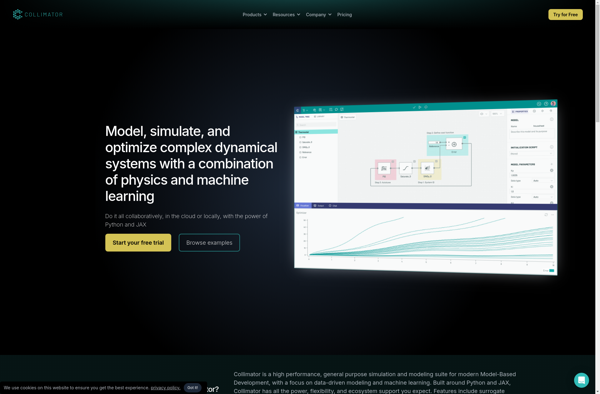
Description: A collimator is a device that narrows a beam of particles or waves. It can be used to align beams or filter out unwanted particles.

JModelica

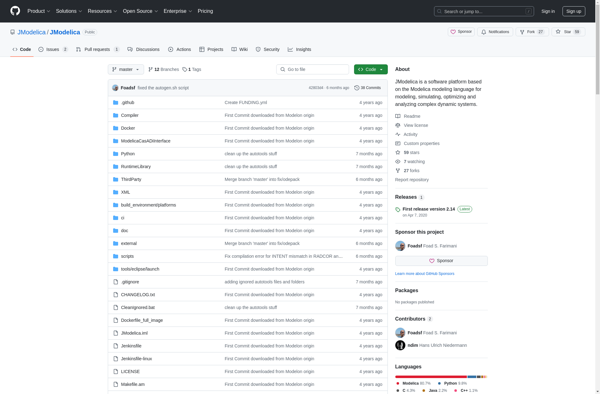
Description: JModelica is an open source platform for modelling and simulation of large-scale dynamic systems using the Modelica modeling language. It facilitates collaborative model-based design. It is aimed at models involving both differential, algebraic, and discrete equations.

Key Features Comparison

Collimator Features

• Aligns radiation beams to shape the beam as needed for different applications
• Filters out radiation particles outside of the desired beam shape
• Adjustable collimator leaves to customize beam shape
• Light field projection to visualize beam shape on patient
• Auto-positioning of leaves based on treatment plan

JModelica Features

• Modeling and simulation of dynamic systems
• Support for Modelica modeling language
• Optimization and symbolic algorithms
• Model export to FMI and Modelica
• Integration with Python and Jupyter notebooks
• Open source and cross-platform

Pros & Cons Analysis

Collimator

Pros

• Precisely shapes radiation dose to target tumor while avoiding healthy tissue
• Reduces radiation exposure and side effects
• Improves treatment accuracy and efficacy
• Easy to use and adjust beam shaping leaves
• Automated leaf positioning saves time

Cons

• High initial cost of system
• Complex calibration and quality assurance testing required
• Limited beam shaping flexibility compared to some other techniques
• Potential for errors in leaf positioning
• Requires skilled staff for operation

JModelica

Pros

• Free and open source
• Support for large and complex models
• Fast simulation of hybrid systems
• Seamless Python integration
• Active development community

Cons

• Limited documentation and examples
• Steep learning curve for Modelica
• Lacks some advanced simulation features
• Not as user friendly as commercial tools

Pricing Comparison

Collimator

• One-time Purchase
• Subscription-Based
• Custom Pricing

JModelica

• Open Source